Lean 4 Datasets

Welcome

This blog post is the first in a series from the G-Research Technology Innovation Group where we share early explorations into Lean 4 (an interactive theorem prover and programming language). Our interest lies in both using Lean 4 for applied mathematics as well as the interection of Lean with LLMs in automated theorem proving.

This first post introduces common datasets one encounters in the literature on Lean 4 and LLMs. Information about these datasets is often scattered across papers and repositories. Our aim isn’t to repeat what already exists or even to organize every last bit in one place, but rather to provide a few high level statistics highlighting insights and background knowledge that may help bridge gaps for newcomers to the field. We assume that many folks, like us, with an ML background will be drawn to the intersection of Lean and AI, and this post aims to help people get started by providing easy, tangible contact with the data used to train and evaluate models in this space.

We’ve compiled various statistics across seventeen sources, covering approximately 530,000 distinct data points.

A Quick Look

Each dataset we present varies in format, size, and emphasis. Before describing the details, let’s just dive in and have a quick look at a small but diverse sample. Use the slider below to flip through a few datapoints.

A Next Look

Here’s another quick visualization of 10% of the data. Use the crossfilter below to select data of interest, and then drill down to a specific datapoint by selecting a row from table underneath.

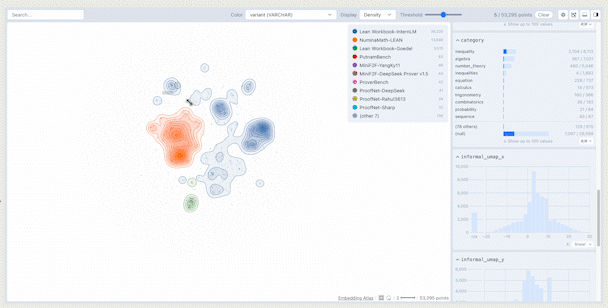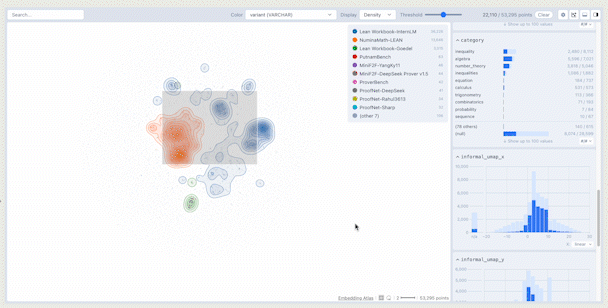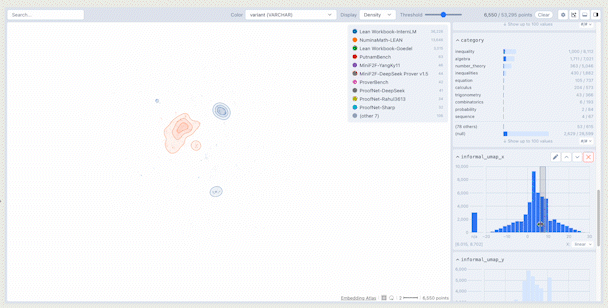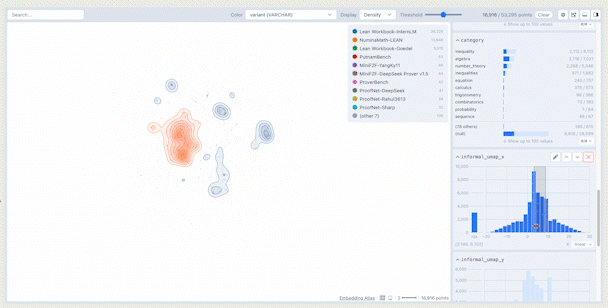
The main display of the crossfilter shows a density plot of the data in embedding space and the side charts show other data associated with each datapoint.

Dataset Structure

Now that we have had a quick look, let’s dive into more details. We distinguish between “datasets” (12 in total) and “dataset variants” (17 in total). A dataset refers to the original announcement or release of a collection of data. A data set variant, on the other hand, is a variant of that dataset that has evolved over time through the work of different authors.

Variants may arise for several reasons — for example, someone might clean up the original data, adapt it to a newer version of Lean 4, or extend it. In some cases, the original dataset may have been incomplete, containing only formal statements without corresponding proofs. Later variants often fill in these gaps by adding proofs once they are discovered.

Each entry in a dataset variant contains, at minimum, a formal Lean 4 theorem statement. Beyond that, it may also include:

• A formal proof the stated theorem
• An informal version of the same statement or proof in natural language.
• Metadata, such as the source of the problem (e.g., a math competition with its name and year, a textbook with author information, or a collection from a website like Art of Problem Solving), the branch of math the problem is related to, whether the problem was in the training or testing split, etc.

Themes

The datasets can be broadly organized as

• Large training datasets (~100k datapoints or more) that were generated by autoformalizers such as NuminaMath-Lean or LeanWorkbook
• Evaluation datasets consisting of 50-500 problems such at MiniF2F, PutnamBench, Combibench, ProverBench, and Proofnet.
• Hand curated datasets such as CompFiles and IMO-Shortlist which tend not to focus on training or evaluating LLMs, but instead are examples of well-written Lean 4 proofs.

In our assessment, PutnamBench is the hardest evalualation in the sense that the fewest number of humans would be able to perform well on this benchmark (and those that did do well would likely have careers as mathematicians). Proofnet pulls exercises from Artin and Munkres and other classics from the undergrad math curriculum. These exercises mostly test understanding and are not as difficult as many of the problems taken from competitions, but do require using the largest number of abstract topics (groups, vector spaces, etc) from Mathlib.

Structure of the Formal Content

The formal Lean4 content of a datapoint is a “whole proof” (e.g. a single single) that nevertheless is typically strcutured in the following format:

• Prelude
  • A set of imports, usually from Mathlib or portions of it, depending on the dataset.
  • open statements – Declarations that bring specific symbols into the current namespace.
• Comments (optional) – Natural language descriptions of the formal content.
• Helpers (rare) – Abbreviations, auxiliary lemmas, or other supporting material. Most datasets omit these.
• Theorem statement – The formal Lean-4 statement of the theorem.
• Proof – This may be a complete formal proof, or simply a placeholder marked with by sorry.

The one universal feature of the formal content across all the sources we consider in this blog is that they can be piped into the Lean 4 compiler for a quick and consistent proof check:

... | lake env lean --stdin --json <other args>

A return code of zero indicates the statement/proof is valid. Otherwise, error messages are provided in json format

Structure of the Informal Content

The informal content of each datapoint varies: it may be missing entirely, consist only of an informal statement, or in some cases include both an informal statement and a complete informal proof.

Catalog

Here are cards for each data source we examined:

TODO List

• Add FATE

Experiments

We ran proof checks on 530,000 items across 12 versions of Lean, from 4.10 through 4.22. Each proof check was executed as a separate invocation of the Lean compiler as discussed above. Alternatives such as REPL-based systems (e.g., Lean Dojo, Pantograph, or Lean REPL) were considered but deemed too fragile and difficult to run realiable across many Lean versions. The direct compiler invocation provides a upper bound on resource utilization.

The workflow began by constructing a dataframe for each dataset-version pair, yielding roughly 6 million entries in total. These entries were then enqueued into AWS SQS for processing, with the entire pipeline executed on AWS.

For execution, we provisioned worker clusters on EC2 using coiled.io. The main instance type we relied on was the c7a.48xlarge, an AMD instance with 192 cores. On startup, each worker installed the required Lean versions (about 400 GB of disk space for the installations), and then began pulling tasks from the queue. Each worker parallelized checks across all cores, ensuring full utilization of the instance.

We typically launched around 80 such instances, which translated to approximately 15,000 concurrent workers. At this scale, the complete run finished in 3–4 hours. Because we relied on a queue-based system, worker failures and transient outages were not problematic. This allowed us to start with a small number of workers to sanity-check outputs, and then dynamically scale up confidently. The design also enabled the use of spot instances, which reduced costs significantly—by roughly 2× to 4×. Under the configuration described here, the entire run cost about $400.

We also benchmarked different configurations. Using ARM- and Intel-based instances with comparable core counts produced similar throughput though were ultimately either more expensive or difficult to provision in large quantities. However, scaling horizontally with many smaller, low-core-count instances introduced inefficiencies. In those cases, runtime and cost could increase by as much as 20×, likely due to contention and memory-related overhead. Larger, high-core-count machines consistently provided the best performance-to-cost ratio(TLDR: use a smaller number of big machines).

def check_proof(
    whole_proof,
    *,
    options: dict[str, str] = None,
    threads: int = None,
    limit_memory_MB: float = None,
    limit_cpu_s: int = None,
    lean_version: str = DEFAULT_LEAN_VERSION,
    cache_dir: Path = None,
    grace: float = 2.0,
    skip_ensure: bool = False,
) -> dict:
    if not skip_ensure:
        ensure_scratch(lean_version, cache_dir)
    cache_dir = resolve_cache_dir(lean_version, cache_dir)
    cwd = str(cache_dir)
    version = safe_run("lake env lean --version", cwd=cwd).strip()
    commit = safe_run("lake env lean -g", cwd=cwd).strip()
    args = []
    args += ["lake", "env", "lean", "--stdin", "--json"]
    if options is not None:
        for k, v in options.items():
            args.append(f"-D {k}={v}")
    if threads is not None:
        args.append(f"--threads={threads}")
    if limit_memory_MB is not None:
        args.append(f"--memory={limit_memory_MB}")
    res = {
        "lean_version": lean_version,
        "full_lean_version": version,
        "commit": commit,
        "whole_proof": whole_proof,
        "threads": threads,
        "limit_memory_MB": limit_memory_MB,
        "limit_cpu_s": limit_cpu_s,
        "options": options,
    }

    def pre_fork():
        # Set the resource limits before forking
        import resource

        if limit_memory_MB is not None:
            resource.setrlimit(
                resource.RLIMIT_AS,
                (limit_memory_MB * 1024 * 1024, limit_memory_MB * 1024 * 1024),
            )
        if limit_cpu_s is not None:
            resource.setrlimit(resource.RLIMIT_CPU, (limit_cpu_s, limit_cpu_s))

    start = time.time()
    process = subprocess.Popen(
        args,
        cwd=cwd,
        preexec_fn=pre_fork,
        stdin=subprocess.PIPE,
        stdout=subprocess.PIPE,
        stderr=subprocess.PIPE,
    )
    # start a thread to monitor the max memory usage
    max_memory = None

    #    mem_log = []
    def monitor_memory():
        try:
            nonlocal max_memory
            _process = psutil.Process(process.pid)
            while _process.is_running():
                mem = memory_usage(_process)
                if max_memory is None or mem > max_memory:
                    max_memory = mem
                if limit_cpu_s is not None:
                    if time.time() - start > limit_cpu_s + grace:
                        print("Killing process due to time limit")
                        _process.kill()
                        return
                time.sleep(0.25)
                _process = psutil.Process(process.pid)  # why is this needed?

        except psutil.NoSuchProcess:
            pass

    monitor_thread = threading.Thread(target=monitor_memory)
    monitor_thread.start()

    comm_timeout = limit_cpu_s + 2 * grace if limit_cpu_s is not None else None
    try:
        stdout, stderr = process.communicate(
            input=whole_proof.encode(), timeout=comm_timeout
        )
    except subprocess.TimeoutExpired:
        stdout, stderr = b"", b""
        try:
            process.kill()
        except:
            pass
    end = time.time()
    monitor_thread.join()
    stdouts = stdout.decode()
    res["stdout"] = stdouts
    res["stderr"] = stderr.decode()
    res["command_str"] = " ".join(args)
    res["command"] = args
    res["returncode"] = process.returncode
    res["time"] = end - start
    res["max_memory"] = max_memory
    
    res["cpu_info"] = cpu_info()
    json_out = []
    json_parsing_problems = []
    for line in stdouts.split("\n"):
        if len(line) == 0:
            continue
        try:
            json_out.append(json.loads(line))
        except json.JSONDecodeError as e:
            json_parsing_problems.append({"line": line, "exception": str(e)})
    res["json_output"] = json_out
    res["json_parsing_problems"] = json_parsing_problems
    return res

Charts

In analyzing these datasets, there were some natural questions that arose:

• Dataset composition: What is included (formal proofs, formal statements, informal statements, informal proofs)?
• Compatibility: How do these datasets hold up across different versions of Lean4, given its rapid release cycle (roughly monthly)?
• Performance costs: How long does it take Lean4 to verify statements or proofs? How much memory does this require?
• Robustness: What kinds of obscure or unexpected errors emerge when running these datasets through Lean4?

These questions matter in part because many training and evaluation methods in this field involve some form of verified reinforcement learning, where models interact directly with Lean 4. Understanding the costs of that interaction — time, memory, and error modes — gives us a baseline for the engineering complexity involved.

Dataset Compatibility Across Lean4 Versions

Lean4 has evolved rapidly, with version changes from 4.10 through 4.22 in the last year.

We evaluated each dataset against these versions to measure:

• How often proofs/statements remain valid across releases.
• The rate at which datasets “decay” (lose compatibility).

Verification Performance

We also measured the time and memory cost of verification:

Below you can use the slider to see how resource utilization changes across Lean 4 versions.

Dig deeper using the interactive crossfilter below by selecting a window in the heatmap or single-clicking bars:

Errors

Examine datapoints that failed to proof check (This is a 10% random sample of all errors. The full set is here)

Outliers: Execution Time

Examine datapoints that were killed for not proof-checking within ~2min.

Outliers: Memory Usage

Examine datapoints with the highest memory utlization.

Conclusion

The goal of this post was to provide a unified entry point for understanding Lean4 datasets from an engineering perspective. While descriptions of these datasets exist in various papers, they are often scattered and rarely discussed in terms of version stability, verification performance, or error robustness.

We hope this overview helps researchers and engineers get oriented in the space more quickly. If you have questions, comments, corrections or would like to collaborate, please don’t hesitate to reach out.

Bibliography